Problem zaokrągleń występuje zawsze, gdy wykonywane są operacje na liczbach rzeczywistych niezależnie od tego, czy robimy je na papierze, liczydłach, kalkulatorze, czy też wykonuje je za nas program komputerowy. My, użytkownicy komputerów, mamy skłonność do całkowitego zaufania temu urządzeniu w przypadku wykonywania przez nie obliczeń. Niestety, w komputerze wynik na przykład takiej operacji jak (20,15*100,0) może nie być równy 2015,0!
Błędy zaokrągleń powstające podczas obliczeń numerycznych prowadzonych w programach komputerowych zależą od:
1. specyfiki komputerowej arytmetyki,
2. przyjętych przez programistów algorytmów obliczeniowych.
*
Arytmetyka w komputerze, czyli jak komputer dodaje, odejmuje, mnoży i dzieli
We współczesnych komputerach zarówno liczby całkowite, jak i liczby rzeczywiste (zmiennoprzecinkowe), zapisywane są w notacji dwójkowej. Oznacza to, że każda liczba przedstawiana jest w postaci kombinacji zer i jedynek - jako suma potęg liczby 2. Elementy pamięci komputerów (zwane słowami), w których przechowywane są liczby, mają z góry określony rozmiar, a więc każda liczba jest reprezentowana przez ustaloną liczbę cyfr i znak. To z kolei znaczy, że obliczenia w komputerze prowadzone są na dyskretnym, skończonym zbiorze liczb.
W przypadku liczb całkowitych zamiana ich wartości z zapisu dziesiętnego, którym się zwykle posługujemy, na binarny, nie powoduje błędów, gdyż każda liczba całkowita z zakresu, jaki udostępnia nam komputer daje się zapisać przy pomocy skończonej liczby tychże zer i jedynek. Na przykład liczba 13 ma postać binarną równą 1101 (1*23 + 1*22+0*21+ 1*20 = 8+ 4 + 0 + 1) , a liczba 2857 - postać 101100101001.
Operacje dodawania i odejmowania liczb całkowitych, jak również mnożenia ich przez potęgę liczby 2 nie generują błędów.
Problem powstaje, gdy zaczynamy operować na liczbach zmiennoprzecinkowych, które pojawiają się już wtedy, gdy zostanie wykonane na przykład dzielenie dwóch liczb całkowitych. Nawet taki prosty ułamek dziesiętny jak 0.1 nie daje się przedstawić w postaci binarnej bez straty dokładności, co prawda niewielkiej, ale jednak. Ułamek ten po przekształceniu do postaci binarnej i z powrotem dziesiętnej, daje w wyniku liczbę 0,0999908 (liczba ta powstała w następujący sposób: 1/16 + 1/32 + 1/256 + 1/512 + 1/4096 + 1/8192 + 1/65536, czyli 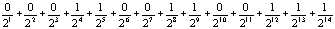 ). Po zaokrągleniu i wyświetleniu liczba ta ma wartość 0.1, ale faktycznie, w komputerze, ma wartość przybliżoną i ta właśnie wartość jest brana do obliczeń. Widać z tego, że wielokrotne użycie tego ułamka może wygenerować dodatkowe błędy.
). Po zaokrągleniu i wyświetleniu liczba ta ma wartość 0.1, ale faktycznie, w komputerze, ma wartość przybliżoną i ta właśnie wartość jest brana do obliczeń. Widać z tego, że wielokrotne użycie tego ułamka może wygenerować dodatkowe błędy.
Błędy powstają także wtedy, gdy komputer wykona operację, której wynikiem jest ułamek o nieskończonym rozwinięciu (np. 0.33333....). Komputer, w którym liczba musi być przedstawiona w ustalonej i ograniczonej długości zastąpi prawdziwy wynik obliczeń liczbą przybliżoną, a to oznacza, że pojawi się błąd zaokrąglenia.
**
Zaokrąglanie liczb w Normie Pro
W Normie Pro sposobem zaokrąglania liczb steruje opcja Zaokrąglanie liczb zgodnie z PN-70-N-02120 z karty 'Ogólne' okna opcji programu. Domyślnie opcja ta jest wyczyszczona, co oznacza, że w Normie Pro stosuje się następujące zasady zaokrąglania liczb:
- Jeśli pierwsza (licząc od lewej strony) z odrzuconych cyfr jest mniejsza od 5, to ostatnia pozostawiona cyfra nie ulega zmianie.
- Jeśli pierwsza (licząc od lewej strony) z odrzuconych cyfr jest większa od 5, to ostatnia pozostawioną cyfrę powiększa się o 1.
- Jeśli pierwsza (licząc od lewej strony) odrzucona cyfra jest równa 5, to niezależnie od tego, co jest za nią, ostatnia pozostawiona cyfra jest zwiększana o 1.
A więc, jeśli na przykład zaokrąglamy liczby do jednego miejsca po przecinku, to:
| 0,05 |
~ 0,1 |
| 0,0501 |
~ 0,1 |
| 0,15 |
~ 0,2 |
| 0,25 |
~ 0,3 |
| 0,450 |
~ 0,5 |
W Polskiej Normie PN-70-N-02120 istnieją trochę inne zasady stosowane w przypadku, gdy zaokrąglanie dotyczy liczb zawierających cyfrę 5 jako pierwszą odrzuconą. Są to zasady następujące:
3.a Jeśli pierwsza (licząc od lewej strony) z odrzuconych cyfr jest równa 5, lecz następuje po niej co najmniej jeszcze jedna cyfra inna niż zero, ostatnią pozostawioną cyfrę powiększa się o 1.
3.b Jeśli pierwsza (licząc od lewej strony) z odrzuconych cyfr jest równa 5 i nie następuje po niej żadna cyfra inna niż zero, to ostatnią pozostawioną cyfrę powiększa się o jednostkę, jeśli jest to cyfra nieparzysta (zero uważa się za cyfrę parzystą). Inaczej mówiąc ostatnia pozostawiona cyfra powinna być parzysta.
Jeśli na przykład zaokrąglamy liczbę do pierwszego miejsca po przecinku, to:
| 0,04 |
~ 0 (zgodnie z zasadą 1) |
| 0,06 |
~ 0,1 (zgodnie z zasadą 2) |
| 0,05 |
~ 0 (zgodnie z zasadą 3.b) |
| 0,0501 |
~ 0,1 (zgodnie z zasadą 3.a) |
| 0,15 |
~ 0,2 (zgodnie z zasadą 3.b) |
| 0,25 |
~ 0,2 (zgodnie z zasadą 3.b) |
| 0,450 |
~ 0,4 (zgodnie z zasadą 3.b) |
W Normie Pro będą prowadzone zaokrąglenia zgodnie z tymi zasadami, jeśli w opcjach programu zostanie zaznaczona opcja Zaokrąglanie liczb zgodnie z PN-70-N-02120 (rys.1).

Rys.1. Karta 'Ogólne' opcji programu, na której wybieramy sposób zaokrąglania liczb.
***
Ustalanie dokładności obliczeń
Jeśli chodzi o ceny i kwoty, to domyślnie zaokrąglane są do dwóch miejsc po przecinku. Pozostałe dokładności obliczeń, czyli precyzję ustala sam użytkownik w opcjach kosztorysu na karcie 'Dokładność prezentacji'. To, jakie dokładności zostaną wybrane odbije się na wielkościach obmiarów, nakładów, wartościach jednostkowych, normach, kosztach jednostkowych i podsumowaniu kosztorysu.
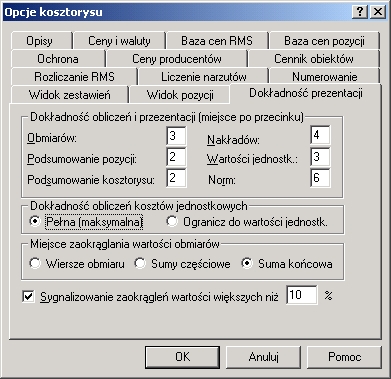
Rys.2. Opcje kosztorysu - karta 'Dokładność prezentacji'
Jeżeli w grupie 'Dokładność obliczeń kosztów jednostkowych' zaznaczymy opcję Ogranicz do wartości jednostk., to precyzja obliczania kosztów jednostkowych zostanie ograniczona do dokładności wyświetlania na ekranie, jeśli zaś opcję Pełna (maksymalna) - wartości te obliczane będą w pełnej precyzji, jaką daje komputer.
Ponieważ obmiary pozycji mogą składać się z różnych wyliczeń cząstkowych, istotne jest jak będą zaokrąglane poszczególne wartości składowe. Do tego celu służą opcje znajdujące się w grupie 'Miejsce zaokrąglania wartości obmiarów'. Określają one, na jakim etapie obliczeń obmiary będą zaokrąglane do precyzji podanej w polu Obmiarów: w grupie 'Dokładność obliczeń i prezentacji'. Jeśli zaznaczymy opcję Wiersze obmiaru:, to do podanej dokładności jako pierwsze zostaną zaokrąglone wiersze obmiaru, i dalej wszystkie następne. Jeżeli zaznaczymy Sumy częściowe:, to wiersze obmiaru będą obliczane z maksymalną dokładnością (ale będą wyświetlone z dokładnością prezentacji), a jako pierwsze zostaną zaokrąglone sumy częściowe. Przy zaznaczonej opcji Suma końcowa, wszystkie obliczenia będą wykonywane z pełną precyzją, a dopiero suma końcowa zostanie zaokrąglona z podaną dokładnością. Jeśli wybierzemy opcję Sumy częściowe lub Suma końcowa, suma wierszy nie musi się równać sumie częściowej (rys.3).
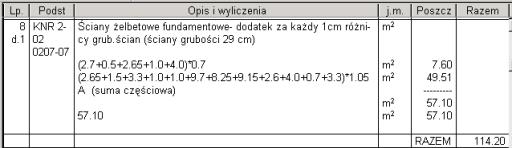
Rys.3. Widać, że suma wierszy w kolumnie 'Poszcz' (7.60+49.51= 57.11) nie jest równa wartości sumy częściowej (=57.10).
Jeśli zaznaczymy opcję Wiersze obmiaru: poszczególne sumy powinny się zgadzać (rys. 4).
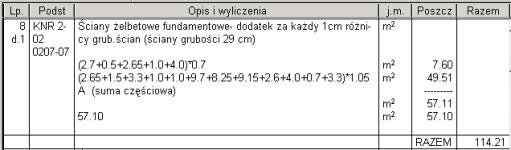
Rys.4.Widać, że suma wierszy w kolumnie 'Poszcz' (7.60+49.51= 57.11) jest równa sumie częściowej (=57.11).
****
Metody liczenia wartości kosztorysu
W NORMIE PRO wartość kosztorysu może być obliczana według cen jednostkowych pozycji lub według wartości nakładów w pozycjach, działach lub całym kosztorysie. Algorytmy te różnią się kolejnością obliczeń i sposobem naliczania narzutów. Opcje sterujące metodami obliczeń znajdują się na karcie 'Liczenie narzutów' okna opcji kosztorysu.
Poniżej znajduje się opis tych metod oraz przedstawienie wyników ich działania na przykładzie.
Przykład:
| Obmiar = 3,982 m3 muru |
-M- Cegła : normatyw = 388,56 szt./m3 cena jednostkowa = 0,97 zł/szt.
Zaprawa: normatyw = 0,261 m3/m3 cena jednostkowa = 149,19 zł/m3 |
| Narzuty: = 13,7 % |
Dokładności: 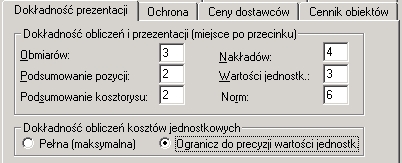 |
I. Kolejność obliczeń w algorytmie liczenia według cen jednostkowych pozycji.
- Koszt jednostkowy nakładu RMS = normatyw (podany z dokładnością ustawioną w opcjach kosztorysu) * cena jednostkowa (automatycznie zaokrąglana do 2 miejsc po przecinku)
Tak wyliczona wartość może być zaokrąglona z dokładnością wartości jednostkowych zależnie od ustawienia opcji Dokładność obliczeń kosztów jednostkowych.
- Wartość nakładów jest sumowana i od sumy zaokrąglonej z dokładnością wartości jednostkowych są liczone narzuty też z dokładnością wartości jednostkowych.
- Tak wyliczona wartość jest mnożona przez wartość obmiaru i daje wartość pozycji (i jest zaokrąglana do precyzji podsumowania pozycji).
Wartości wszystkich pozycji są sumowane (z zaokrągleniem do precyzji podsumowania kosztorysu).
| Aby program liczył według tego algorytmu, na karcie 'Liczenie narzutów' powinna zostać zaznaczona opcja Dla kosztów jednostkowych. |
Dla naszego przykładu algorytm będzie wyglądał następująco:
| Koszt jednostkowy: |
Cegła |
= 388,56 * 0,97 = 376,9032 |
~376,903 (zaokrąglenie do 3 miejsc) |
| |
Zaprawa |
= 0,261*149,19 = 10,16297199 |
~10,163 (zaokrąglenie do 3 miejsc) |
| Wartość nakładów |
= 376,903 + 10,163 = 387,066 |
| Narzuty w pozycji |
= 387,066 * 0,137 = 53,028042 |
~53,028 (zaokrąglenie do 3 miejsc) |
| Wartość pozycji |
= (387,066+53,028)*3,982 = 1752,454308 |
~1752,45 (zaokrąglenie do 2 miejsc) |
II. Kolejność obliczeń w algorytmie liczenia według wartości nakładów w pozycjach, działach lub całym kosztorysie.
- Koszt jednostkowy nakładu RMS = normatyw (podany z dokładnością ustawioną w opcjach kosztorysu) * cena jednostkowa (zaokrąglona do 2 miejsc)
Tak wyliczona wartość może być zaokrąglona z dokładnością wartości jednostkowych (podanej w opcjach kosztorysu) zależnie od ustawienia opcji Dokładność obliczeń kosztów jednostkowych.
- Wartość nakładu RMS = koszt jednostkowy * wartość obmiaru; tak wyliczona wartość jest zaokrąglana z precyzją podsumowania pozycji.
- Wartości nakładów w pozycji (dziale lub całym kosztorysie) jest sumowana i wyliczane są narzuty z precyzją podsumowania pozycji (lub podsumowania kosztorysu).
Wartości wyliczone w pozycjach lub działach są sumowane (z zaokrągleniem do precyzji podsumowania kosztorysu).
| Aby program liczył według tego algorytmu, na karcie 'Liczenie narzutów' powinna zostać wyczyszczona opcja Dla kosztów jednostkowych. |
Dla naszego przykładu algorytm będzie wyglądał następująco:
| Koszt jednostkowy: |
Cegła |
= 388,56 * 0,97 = 376,9032 |
~376,903 (zaokrąglenie do 3 miejsc) |
| Wartość nakładu |
= 376,903*3,982 = 1500,827746 |
~500,83 (zaokrąglenie do 2 miejsc) |
| Koszt jednostkowy |
Zaprawa |
= 0,261 * 149,19 = 10,16297199 |
~10,163 (zaokrąglenie do 3 miejsc) |
| Wartość nakładu |
= 10,163 * 3,982 = 40,469066 |
~40,47 (zaokrąglenie do 2 miejsc) |
| Wartość nakładów w pozycji |
= 1500,83 + 40,47 = 1541,30 |
|
| Narzuty dla pozycji |
= 1541,30 * 0,137 = 211,1581 |
~211,158 (zaokrąglenie do 3 miejsc) |
| Wartość pozycji |
= 1541,30 + 211,158 = 1752,458 |
~1752,46 (zaokrąglenie do 2 miejsc) |
Z wyliczeń przeprowadzonych na powyższych przykładach widać, że wartości pozycji różnią się w zależności od przyjętego algorytmu. W przypadku gdy w kosztorys zawiera wiele pozycji, różnice te mogą się sumować, dając tym samym różne wartości całego kosztorysu. Przeważnie tak jest, że część wartości jest zaokrąglana w górę, część w dół i błędy zaokrągleń częściowo się znoszą, niemniej jednak trzeba brać pod uwagę możliwość wystąpienia niezgodności. Dlatego też bardzo ważne jest, aby uzgodnić z inwestorem, jaką metodą będzie liczony kosztorys i z jaką precyzją będą obliczane wartości pośrednie.
*****
Kontrola procesów obliczeniowych i sygnalizowanie niezgodności
Błędy zaokrągleń i różnice w wartościach zależne od przyjętego algorytmu obliczeniowego uwydatniają się szczególnie w przypadku przeliczania kosztorysu, na przykład przy zmianie typu kosztorysu ze zwykłego na inwestorski, wtedy gdy do kosztorysu zostały wstawione kosztorysy składowe o innych ustawieniach opcji niż w kosztorysie głównym, oraz wyboru sposobu obliczania narzutów, gdy na podstawie kosztorysu zwykłego tworzony jest kosztorys ofertowy.
I. Kontrola wartości kosztów jednostkowych i norm
Do kontroli wartości kosztów jednostkowych i norm wyliczanych podczas przeliczania kosztorysu warto włączyć opcję Sygnalizowanie zaokrągleń wartości większych niż, znajdującą się na karcie 'Dokładność prezentacji'. Wtedy, jeśli w procesie przeliczania wartość zaokrąglona będzie różnić się od pierwotnej o więcej niż określony procent, zostanie wyświetlony odpowiedni komunikat (rys. 5).
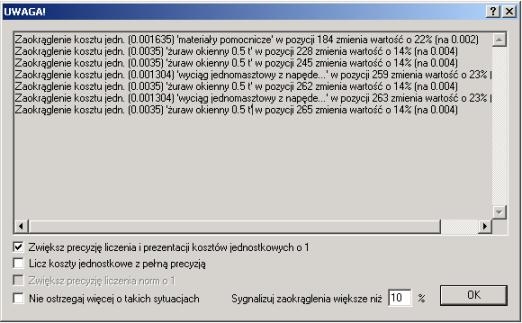
Rys.5. Przykładowy komunikat wyświetlony po zmianie rodzaju kosztorysu ze zwykłego na kosztorys inwestorski.
Gdy komunikat z listą ostrzeżeń pojawi się pierwszy raz, można w nim skorygować opcje prezentacji wartości znajdujące się w opcjach kosztorysu na karcie 'Dokładność prezentacji'. Jeśli na przykład widzimy, że różnice wartości kosztów jednostkowych są zbyt duże, możemy zwiększyć dokładność o rząd wielkości zaznaczając opcję Zwiększ precyzję liczenia i prezentacji kosztów jednostkowych o 1 i/lub włączyć opcję obliczania ich z pełną precyzją (Licz koszty jednostkowe z pełną precyzją). Jeśli błędy przeliczania wartości norm przekraczają założony procent, możemy zaznaczyć opcję Zwiększ precyzję liczenia norm o 1, co spowoduje zwiększenie dokładności obliczeń i prezentacji norm o rząd wielkości.
Jeśli nie chcemy, aby okno z ostrzeżeniami było pokazywane, zaznaczamy opcję Nie ostrzegaj więcej o takich sytuacjach.
Opcja Sygnalizuj zaokrąglenia większe niż odpowiada tej samej opcji ustawianej na karcie 'Dokładność prezentacji' w oknie opcji kosztorysu.
II. Kontrola wartości kosztorysu złożonego
Jeśli tworzymy kosztorys złożony z kilku innych kosztorysów i opcje kosztorysu głównego różnią się od opcji przyjętych dla kosztorysów składowych, program wyprowadza ostrzeżenie i informuje, jakie opcje zostały inaczej określone (rys.6). Z powodu różnic opcji wartość kosztorysu złożonego może nie być równa sumie wartości kosztorysów składowych.
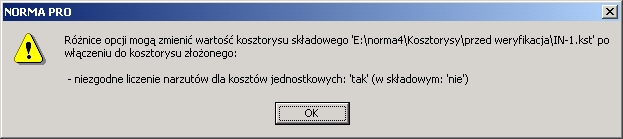
Rys.6. Komunikat wyświetlony po zmianie rodzaju kosztorysu ze zwykłego na inwestorski.
III. Kontrola obliczania narzutów dla kosztorysu ofertowego
Ażeby uniknąć nieporozumień w przypadku tworzenia kosztorysów ofertowych (dla przetargu podlegającego przepisom ustawy o zamówieniach publicznych), użytkownik ma możliwość wyboru szablonu obliczeń dla kosztorysów tego typu oraz może uaktywnić opcję generowania ostrzeżeń dotyczących wydruków dla różnych sposobów obliczania narzutów.
Szablon obliczania narzutów wybieramy w polu kosztorysu Szablon liczenia narzutów:. Jeśli wybierzemy Zamówienia publiczne (oferta), to automatycznie zostaną zaznaczone właściwe opcje, których nie będzie można zmienić. Jeśli wybierzemy Narzuty liczone dla całego kosztorysu, to narzuty będę liczone od wartości zsumowanych kosztów w całym kosztorysie. Jeśli w polu Szablon liczenia narzutów: wybierzemy Ustawienia własne, to opcje staną się dostępne i będzie można określić własny sposób obliczania narzutów.
Dokładne wyjaśnienie konsekwencji wyboru określonych ustawień narzutów znajdziecie Państwo w rozdziale NARZUTY podręcznika użytkownika programu NORMA PRO.
Jeśli w kosztorysach sami ustalamy opcję liczenia narzutów, dobrze jest zaznaczyć pole wyboru Sprawdzanie sposobu liczenia narzutów na karcie 'Liczenie narzutów' i wtedy program będzie generował ostrzeżenia w przypadku wystąpienia niedokładności wyliczeń wartości pozycji i podsumowań, gdy będziemy drukować kosztorys ofertowy (rys. 7). W dolnej części okna kontroli wydruków wyświetlana jest informacja o tym, z jakimi niedokładnościami mamy do czynienia.
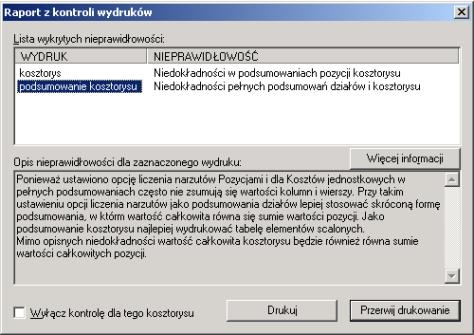
Rys.7. Przykładowe ostrzeżenia i informacje generowane przed wydrukiem kosztorysu.
******
Kosztorysowanie ofertowe w zamówieniach publicznych
Według opinii Urzędu Zamówień Publicznych z maja 2003 r. oraz wyroku Zespołu Arbitrów dotyczących cen przedstawianych w ofercie: "Co do zasady ... cena przedstawiona przez oferenta w ofercie powinna zostać określona z dokładnością do drugiego miejsca po przecinku."
Zasada ta wynika z faktu, że rozliczenia między stronami umowy muszą odbywać się w jednostkach pieniężnych Rzeczypospolitej Polskiej, czyli w złotych i groszach. Jak w tym wypadku tworzyć kosztorysy ofertowe odpowiadające ustawie o zamówieniach publicznych? Najlepiej byłoby trzymać się powyższej zasady[1].
W rozporządzeniu Ministra Finansów z dnia 22 marca 2002r. w sprawie wykonania niektórych przepisów ustawy o podatku od towarów i usług oraz o podatku akcyzowym (§35 ust.5, Dz.U. nr 27, poz. 268 z późn.zm.) podany jest algorytm, według którego zaokrąglane są kwoty na fakturach: "Kwoty wykazywane w fakturze zaokrągla się do pełnych groszy, przy czym końcówki poniżej 0,5 grosza pomija się, a końcówki 0,5 grosza i wyższe zaokrągla się do 1 grosza."
Opisane wyżej reguły są przyjęte w Normie Pro jako domyślne: kwoty wszystkich podsumowań są zaokrąglane do dwóch miejsc po przecinku, a sposób zaokrąglania jest identyczny z zasadami przyjętymi w ww. rozporządzeniu (opcja Zaokrąglanie liczb zgodnie z PN-70-N-02120 wyczyszczona).
Powyższe wyjaśnienia zostały opracowane na podstawie artykułu pt. "ZAMÓWIENIA PUBLICZNE. OKREŚLANIE CENY W OFERCIE. Nie ma tysięcznych części złotego, ale..." zamieszczonego w Gazecie Prawnej nr 120 (976) z dn. 23 czerwca 2003 r.
1) Uwaga - Ta sama opinia UZP dopuszcza składanie ofert z cenami określonymi w tysięcznych częściach złotego - na przykład w przypadku, gdy "...oferenci dokonują obliczenia ceny oferty na podstawie różnorodnych składników (materiały użyte do wykonania zamówienia, robocizna, sprzęt). (...) Wówczas wydaje się dopuszczalne stosowanie w formularzu składników cenotwórczych określonych w tysięcznych częściach złotego o ile cena ostateczna (końcowa, wynik kalkulacji) płacona przez zamawiającego, określona zostanie z dokładnością do dwóch miejsc po przecinku. Przyjmuje się bowiem, iż wskazane w formularzu ceny jednostkowe mają jedynie znaczenie kalkulacyjne. Są więc mnożnikiem, który służyć ma do odpowiedniego obliczenia wynagrodzenia za wykonaną usługę, dostawę czy robotę budowlaną ..."