Jak oszacować koszty budowy we wstępnej fazie podejmowania decyzji (cz. II)

Wpływ efektu skali na koszty budowy

Rozkład liniowy

O ile ocena wysokości kosztu budowy w zależności od jej wielkości sprawdza się w praktycznym stosowaniu dla obiektów, których wszystkie koszty rozkładają się liniowo w stosunku do rozmiarów obiektu, to jest ona nieskuteczna tam, gdzie koszt jednostkowy spada tylko do pewnej optymalnej wielkości wytwarzania, a po jej przekroczeniu raptownie wzrasta na skutek konieczności dodatkowego wyposażenia zakładu, (np. trzeba zainstalować dodatkowy transformator, dodatkowe kotły centralnego ogrzewania, dodatkowy agregat klimatyzacyjny), co podwyższa jednostkowe koszty wytwarzania o dodatkowe koszty kapitałowe i amortyzację.

Dla obliczenia tych zależności niezbędne są dane empiryczne w celu ustalenia optymalnej wielkości różnych typów instalacji - dla stwierdzenia, która z instalacji zapewnia najniższe koszty jednostkowe.

Do obliczenia przyjmijmy, że X jest zmienną reprezentującą zdolności produkcyjne, a Y określa koszty robót budowlanych.
Liniowe równanie tych relacji wyraża wzór

Y = a + b*X

gdzie a i b są wielkościami określonymi na podstawie danych empirycznych.

Zauważmy, że w tym równaniu stałe koszty a dla x = 0 są wielkościami niezależnymi od wielkości obiektu (koszty organizacji i urządzenia placu budowy, wydzielone w przedmiarze jako samodzielna pozycja), co przedstawia wykres osi Y, jak niżej

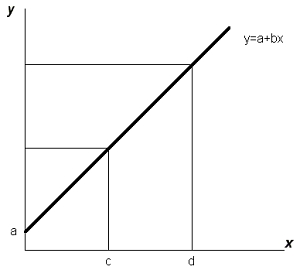
W ten sposób koszt budowy budynku można oszacować na podstawie liniowej relacji pomiędzy kosztami bezpośrednimi przypadającymi na m² powierzchni podłogi, zwiększając je o koszty stałe a.

Rozkład nieliniowy

Zależność nieliniowa ma miejsce, gdy koszty obiektu obejmują koszty stałe instalacji i urządzeń (transformatory, kotły, c.o. i c.w., stacja klimatyzacyjna). Te koszty stałe rozkładają się na zwiększoną powierzchnię lub kubaturę w formie nieliniowej. Równanie nieliniowych relacji między wielkością obiektu i tymi kosztami przedstawia w postaci logarytmicznej wzór:

lny = lna + b*lnx

gdzie a i b są określone na podstawie danych historycznych(?) dla 0 <b <1
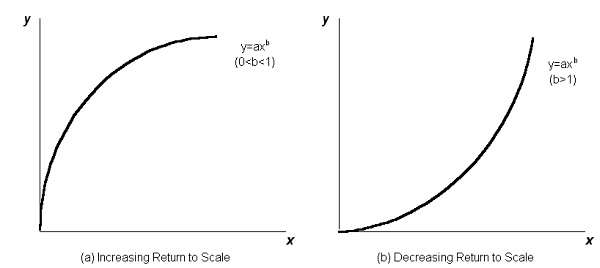
Równanie stanowi podstawę do obliczenia zależności pomiędzy wielkością obiektu i kosztami dla przypadku zwiększenia lub zmniejszenia jego skali, czyli wielkości, co pokazują wykresy nieliniowej zależności pomiędzy wielkością i kosztami (zwiększenie lub zmniejszenie efektu skali).

Praktycznie biorąc, nieliniowe relacje kosztów badamy przy oszacowaniu kosztów nowego obiektu przetwórczego, poczynając od znanych kosztów istniejącego obiektu o określonej wielkości. Przykładowo, jeżeli przyjmiemy że y_n to koszty istniejącego obiektu o pojemności Q_n, a y to szacunkowe koszty nowego obiektu, który ma zdolność Q, to możemy obliczyć na podstawie danych empirycznych, że:
 

Y = y_n (Q/Q_n)^m

gdzie m zwykle waha się od 0,5 do 0,9 w zależności od konkretnego typu obiektu.

Niżej przedstawiam, jako przykład, określenie wielkości parametru „m” dla oczyszczalni ścieków

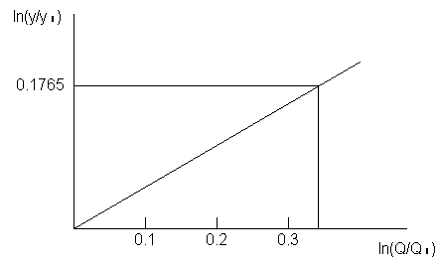
Wg empirycznych danych o kosztach oczyszczalni ścieków wykreślone zostały na skali ln(Q/Q_n) i ln(y/y_n) oraz zależność liniowa pomiędzy tymi wskaźnikami.

W celu szybkich obliczeń możemy zastosować formułę równań nieliniowych wg wzoru

ln(y/y_n) = m * ln(Q/Q_n)

Tym samym parametr m obliczamy jak niżej:

m = 0,1765 / 0,301 = 0,585

Z obliczenia wynika, że dla parametru m = 0,585 koszt zakładu wzrasta 1,5 razy, przy dwukrotnym wzroście przepustowości.
Poniżej cytuję dane o wielkości parametru „m” dla poszczególnych instalacji oczyszczalni ścieków.
Parametr „m” stanowi miarę skali związaną z budową dodatkowych możliwości dla przyszłego wzrostu zdolności przetwórczych i niezawodności projektowanej oczyszczalni ścieków. Gdy „m” jest zbliżone do 1, koszt jest wprost proporcjonalny do wielkości projektowanej oczyszczalni. Natomiast gdy „m” kształtuje się poniżej jedności, istnieje podstawa do zwiększenia projektu o dodatkowe pojemności w celu zwiększenia efektu ekonomicznego skali.
Niżej przedstawiam praktyczne zastosowanie metody wykładniczego oszacowania kosztów na podstawie danych statystycznych wg wzoru

y = k*q^m

gdzie:
y - szacowany koszt nowej instalacji
k - koszt instalacji istniejącej
q - wydajność nowej instalacji
m - parametr

Jeśli parametr „m” i koszty są znane dla danego typu instalacji, to koszty y dla proponowanej nowej placówki o wielkości Q można łatwo obliczyć czerpiąc dane z tabeli kosztów i parametrów instalacji już zrealizowanych jak niżej:

Jako przykład zastosowania podanego wyżej wzoru weźmy instalację sedymentacji (koszt = 399 dolarów za stopę kwadratową, parametr m = 0,60). Dla planowanej nowej oczyszczalni, wyposażonej w instalację sedymentacji o wielkości 15.000 stóp², szacowany koszt w $ będzie wynosił:

y = [399 * 15.000]^0,60 = 128.000 [$]

Dla obliczenia wyników równania wykładniczego stosujemy instrumentarium matematyczne arkusza kalkulacyjnego komputera osobistego.

Bibliografia:

1. Project Management for Construction Fundamental Concepts for Owners, Engineers, Architects and Builders by Chris Hendrickson, Department of Civil and Environmental Engineering, Carnegie Mellon University, Pittsburgh, PA l52l3 Copyright C. Hendrickson 1998
2. Clark, F.D., and A.B. Lorenzoni, Applied Cost Engineering, Marcel Dekker, Inc., New York, 1978
3. Clark, J.E., Structural Concrete Cost Estimating, McGraw-Hill, Inc., New York, 1983
4. Diekmann, J.E., "Probabilistic Estimating: Mathematics and Applications" ASCE Journal of Construction Engineering and Management, Vol. 109, 1983, pp. 297-308
5. Humphreys, K.K. (ed.) Project and Cost Engineers' Handbook (sponsored by American Association of Cost Engineers), 2nd Ed., Marcel Dekker, Inc., New York, 1984
6. Maevis, A.C., "Construction Cost Control by the Owners" ASCE Journal of the Construction Division, Vol. 106, 1980, pp. 435-446
7. Wohl, M. and C. Hendrickson, Transportation Investment and Pricing Principles, John Wiley & Sons, New York, 1984